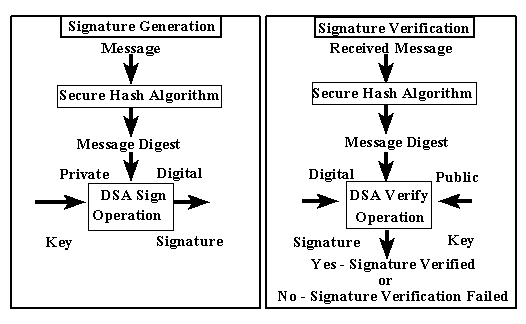
Figure 1: Using the SHA with the DSA
26 June 1998
Source:
http://www.itl.nist.gov/div897/pubs/fip186.htm
Name of Standard: Digital Signature Standard (DSS).
Category of Standard: Computer Security; Cryptography.
Explanation: This Standard specifies a Digital Signature Algorithm
(DSA) appropriate for applications requiring a digital rather than written
signature. The DSA digital signature is a pair of large numbers represented
in a computer as strings of binary digits. The digital signature is computed
using a set of rules (i.e., the DSA) and a set of parameters such that the
identity of the signatory and integrity of the data can be verified. The
DSA provides the capability to generate and verify signatures. Signature
generation makes use of a private key to generate a digital signature. Signature
verification makes use of a public key which corresponds to, but is not the
same as, the private key. Each user possesses a private and public key pair.
Public keys are assumed to be known to the public in general. Private keys
are never shared. Anyone can verify the signature of a user by employing
that user's public key. Signature generation can be performed only by the
possessor of the user's private key.
A hash function is used in the signature generation process to obtain a condensed
version of data, called a message digest (see Figure 1). The message digest
is then input to the DSA to generate the digital signature. The digital signature
is sent to the intended verifier along with the signed data (often called
the message). The verifier of the message and signature verifies the signature
by using the sender's public key. The same hash function must also be used
in the verification process. The hash function is specified in a separate
standard, the Secure Hash Standard (SHS), FIPS 180. Similar procedures may
be used to generate and verify signatures for stored as well as transmitted
data.

Approving Authority: Secretary of Commerce.
Maintenance Agency: U.S. Department of Commerce, National Institute
of Standards and Technology (NIST), Computer Systems Laboratory (CSL).
Applicability: This standard is applicable to all Federal departments
and agencies for the protection of unclassified information that is not subject
to section 2315 of Title 10, United States Code, or section 3502(2) of Title
44, United States Code. This standard shall be used in designing and implementing
public-key based signature systems which Federal departments and agencies
operate or which are operated for them under contract. Adoption and use of
this standard is available to private and commercial organizations.
Applications: The DSA authenticates the integrity of the signed data
and the identity of the signatory. The DSA may also be used in proving to
a third party that data was actually signed by the generator of the signature.
The DSA is intended for use in electronic mail, electronic funds transfer,
electronic data interchange, software distribution, data storage, and other
applications which require data integrity assurance and data origin
authentication.
Implementations: The DSA may be implemented in software, firmware,
hardware, or any combination thereof. NIST is developing a validation program
to test implementations for conformance to this standard. Information about
the planned validation program can be obtained from the National Institute
of Standards and Technology, Computer Systems Laboratory, Attn: DSS Validation,
Gaithersburg, MD 20899.
Export Control: Implementations of this standard are subject to Federal
Government export controls as specified in Title 15, Code of Federal Regulations,
Parts 768 through 799. Exporters are advised to contact the Department of
Commerce, Bureau of Export Administration for more information.
Patents: The Department of Commerce is not aware of any patents that
would be infringed by this standard.
Implementation Schedule: This standard becomes effective December
1, 1994.
Specifications: Federal Information Processing Standard (FIPS186)
Digital Signature Standard (DSS), (affixed).
Cross Index:
Qualifications: The security of a digital signature system is dependent
on maintaining the secrecy of users' private keys. Users must therefore guard
against the unauthorized acquisition of their private keys. While it is the
intent of this standard to specify general security requirements for generating
digital signatures, conformance to this standard does not assure that a
particular implementation is secure. The responsible authority in each agency
or department shall assure that an overall implementation provides an acceptable
level of security. This standard will be reviewed every five years in order
to assess its adequacy.
Waiver Procedure: Under certain exceptional circumstances, the heads
of Federal departments and agencies may approve waivers to Federal Information
Processing Standards (FIPS). The head of such agency may redelegate such
authority only to a senior official designated pursuant to section 3506(b)
of Title 44, United States Code. Waiver shall be granted only when:
Agency heads may act upon a written waiver request containing the information
detailed above. Agency heads may also act without a written waiver request
when they determine that conditions for meeting the standard cannot be met.
Agency heads may approve waivers only by a written decision which explains
the basis on which the agency head made with required finding(s). A copy
of each decision, with procurement sensitive or classified portions clearly
identified, shall be sent to: National Institute of Standards and Technology;
ATTN: FIPS Waiver Decisions, Technology Building, Room B-154, Gaithersburg,
MD 20899.
In addition, notice of each waiver granted and each delegation of authority
to approve waivers shall be sent promptly to the Committee on Government
Operations of the House of Representatives and the Committee on Government
Affairs of the Senate and shall be published promptly in the Federal Register.
When the determination on a waiver applies to the procurement of equipment
and/or services, a notice of the waiver determination must be published in
the Commerce Business Daily as a part of the notice of solicitation for offers
of an acquisition or, if the waiver determination is made after that notice
is published, by amendment to such notice.
A copy of the waiver, any supporting documents, the document approving the
waiver and any accompanying documents, with such deletions as the agency
is authorized and decides to make under 5 United States Code Section 552(b),
shall be part of the procurement documentation and retained by the agency.
Where to Obtain Copies of the Standard: Copies of this publication
are for sale by the National Technical Information Service, U.S. Department
of Commerce, Springfield, VA 22161. When ordering, refer to Federal Information
Processing Standards Publication 186 (FIPSPUB186), and identify the title.
When microfiche is desired, this should be specified. Prices are published
by NTIS in current catalogs and other issuances. Payment may be made by check,
money order, deposit account or charged to a credit card accepted by NTIS.
1. INTRODUCTION
This publication prescribes the Digital Signature Algorithm (DSA) for digital
signature generation and verification. Additional information is provided
in Appendices 1 through 5.
2. GENERAL
When a message is received, the recipient may desire to verify that the message
has not been altered in transit. Furthermore, the recipient may wish to be
certain of the originator's identity. Both of these services can be provided
by the DSA. A digital signature is an electronic analogue of a written signature
in that the digital signature can be used in proving to the recipient or
a third party that the message was, in fact, signed by the originator. Digital
signatures may also be generated for stored data and programs so that the
integrity of the data and programs may be verified at any later time.
This publication prescribes the DSA for digital signature generation and
verification. In addition, the criteria for the public and private keys required
by the algorithm are provided.
3. USE OF THE DSA ALGORITHM
The DSA is used by a signatory to generate a digital signature on data and
by a verifier to verify the authenticity of the signature. Each signatory
has a public and private key. The private key is used in the signature generation
process and the public key is used in the signature verification process.
For both signature generation and verification, the data which is referred
to as a message, M, is reduced by means of the Secure Hash Algorithm (SHA)
specified in FIPS YY. An adversary, who does not know the private key of
the signatory, cannot generate the correct signature of the signatory. In
other words, signatures cannot be forged. However, by using the signatory's
public key, anyone can verify a correctly signed message.
A means of associating public and private key pairs to the corresponding
users is required. That is, there must be a binding of a user's identity
and the user's public key. This binding may be certified by a mutually trusted
party. For example, a certifying authority could sign credentials containing
a user's public key and identity to form a certificate. Systems for certifying
credentials and distributing certificates are beyond the scope of this standard.
NIST intends to publish separate document(s) on certifying credentials and
distributing certificates.
4. DSA PARAMETERS
The DSA makes use of the following parameters:
L for 512 = < L = <1024 and L a multiple of 64
160
In the above, k-1 is the multiplicative inverse
of k, mod q; i.e., (k-1 k) mod q = 1 and 0
If v = r', then the signature is verified and the verifier can have high
confidence that the received message was sent by the party holding the secret
key x corresponding to y. For a proof that v = r' when M' = M, r' = r, and
s' = s, see Appendix1.
This appendix is for informational purposes only and is not required to meet
the standard.
The purpose of this appendix is to show that if M' = M, r' = r and s' = s
in the signature verification then v = r'. We need the following easy result.
LEMMA. Let p and q be primes so that q divides p - 1, h a positive
integer less than p, and g = h(p-1)/q mod
p. Then gq mod p = 1, and if m mod q = n mod
q, then gm mod p =
gn mod p.
Proof: We have
gq mod p = (h(p-
1)/q mod p)q mod p
by Fermat's Little Theorem. Now let m mod q = n mod q, i.e., m = n + kq for
some integer k. Then
gm mod p =
gn+kq mod p
since gq mod p = 1.
We are now ready to prove the main result.
THEOREM. If M' = M, r' = r, and s' = s in the signature verification,
then v = r'.
Proof: We have
Now y = gx mod p, so that by the lemma,
Also
Hence
Thus by the lemma,
This appendix includes algorithms for generating the primes p and q used
in the DSA. These algorithms require a random number generator (see Appendix
3), and an efficient modular exponentiation algorithm. Generation of p and
q shall be performed as specified in this appendix, or using other FIPS approved
security methods.
In order to generate the primes p and q, a primality test is required.
There are several fast probabilistic algorithms available. The following
algorithm is a simplified version of a procedure due to M.O. Rabin, based
in part on ideas of Gary L. Miller. [See Knuth, The Art of Computer Programming,
Vol. 2, Addison-Wesley, 1981, Algorithm P, page 379.] If this algorithm is
iterated n times, it will produce a false prime with probability no greater
than 1/4n. Therefore, n > or = to 50 will
give an acceptable probability of error. To test whether an integer is prime:
The DSS requires two primes, p and q, satisfying the following three conditions:
L for a specified L, where L = 512 + 64j for some 0
This prime generation scheme starts by using the SHA and a user supplied
SEED to construct a prime, q, in the range
2159
An integer x in the range 0
Conversely, a g-long sequence of bits { x1,...,xg } is converted to an integer
by the rule
Note that the first bit of a sequence corresponds to the most significant
bit of the corresponding integer and the last bit to the least significant
bit.
Let L - 1 = n*160 + b, where both b and n are integers and 0
Any implementation of the DSA requires the ability to generate random or
pseudorandom integers. Such numbers are used to derive a user's private key,
x, and a user's per message secret number, k. These randomly or pseudorandomly
generated integers are selected to be between 0 and the 160- bit prime q
(as specified in the standard). They shall be generated by the techniques
given in this appendix, or using other FIPS approved security methods.
One FIPS approved pseudorandom integer generator is supplied in Appendix
C of ANSI X9.17, "Financial Institution Key Management (Wholesale)."
Other pseudorandom integer generators are given in this appendix. These permit
generation of pseudorandom values of x and k for use in the DSA. The algorithm
in section 3.1 may be used to generate values for x. An algorithm for k and
r is given in section 3.2. The latter algorithm allows most of the signature
computation to be precomputed without knowledge of the message to be signed.
The algorithms employ a one-way function G(t,c), where t is 160 bits, c is
b bits (160 ó b ó 512) and G(t,c) is 160 bits. One way to construct
G is via the Secure Hash Algorithm (SHA), as defined in the Secure Hash Standard
(SHS). The 160-bit message digest output of the SHA algorithm when message
M is input is denoted by SHA(M). A second method for constructing G is to
use the Data Encryption Standard (DES). The construction of G by these techniques
is discussed in sections 3.3 and 3.4 of this appendix.
In the algorithms in sections 3.1 and 3.2, a secret b-bit seed-key is used.
The algorithm in section 3.1 optionally allows the use of a user provided
input. If G is constructed via the SHA as defined in section 3.3, then b
is between 160 and 512. If DES is used to construct G as defined in section
3.4, then b is equal to 160.
Let x be the signer's private key. The following may be used to generate
m values of x:
This algorithm can be used to precompute k, k-1, and r for m messages at
a time. Algorithm:
As an option, one may wish to check if r = 0 or s = 0. If either r = 0 or
s = 0, a new value of k should be generated and the signature should be
recalculated (it is extremely unlikely that r = 0 or s = 0 if signatures
are generated properly).
The signature is transmitted along with the message to the verifier.
6. SIGNATURE VERIFICATION
Prior to verifying the signature in a signed message, p, q and g plus the
sender's public key and identity are made available to the verifier in an
authenticated manner.
Let M', r' and s' be the received versions of M, r, and s, respectively,
and let y be the public key of the signatory. To verifier first checks to
see that 0
If v does not equal r', then the message may have been modified, the message
may have been incorrectly signed by the signatory, or the message may have
been signed by an impostor. The message should be considered invalid.
Step 9. If i
160
160.
Once this is accomplished, the same SEED value is used to construct an X
in the range 2L-1
160.
and let X = W + 2L-1. Note that 0
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
(1) A robust primality test is one where the
probability of a non-prime number passing the test is at most
2-80.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
This is the initial value for H0 || H1 || H2 || H3 || H4 in the SHS.
This is a cyclic shift of the initial value for H0 || H1 || H2 || H3 || H4
in the SHS.
Step 3 permits precomputation of the quantities needed to sign the next m messages. Step 4 can begin whenever the first of these m messages is ready. The execution of step 4 can be suspended whenever the next of the m messages is not ready. As soon as steps 4 and 5 have completed, step 3 can be executed, and the results saved until the first member of the next group of m messages is ready.
In addition to space for KKEY, two arrays of length m are needed to store r0 , ... rm-1 and k0-1, ... , km-1 -1 when they are computed in step 3. Storage for s0 , ... , sm-1 is only needed if the signatures for a group of messages are stored; otherwise sj in step 4 can be replaced by s and a single space allocated.
G(t,c) may be constructed using steps (a) - (e) in section 7 of the Specifications for the Secure Hash Standard. Before executing these steps, {Hj} and M1 must be initialized as follows:
Then steps (a) through (e) of section 7 are executed, and G(t,c) is the 160 bit string represented by the five words:
at the end of step (e).
Let a XOR b denote the bitwise exclusive-or of bit strings a and b. Suppose a1, a2, b1, b2 are 32-bit strings. Let b1' be the 24 least significant bits of b1. Let K = b1' || b2 and A = a1 || a2. Define
In the above, DESK(A) represents ordinary DES encryption of the 64-bit block A using the 56-bit key K. Now suppose t and c are each 160 bits. To compute G(t,c):
This appendix is for informational purposes only and is not required to meet the standard.
The algorithms given in this appendix may be used to generate the quantities g, k-1, and s-1 used in the DSS.
To generate g:
To compute the multiplicative inverse n-1
mod q for n with 0
Step 1. Set i = q, h = n, v = 0, and d = 1.
Step 2. Let t = i DIV h, where DIV is defined as integer division.
Step 3. Set x = h.
Step 4. Set h = i - tx.
Step 5. Set i = x.
Step 6. Set x = d.
Step 7. Set d = v - tx.
Step 8. Set v = x.
Step 9. If h > 0, go to step 2.
Step 10. Let n-1 = v mod q. Note that in step
10, v may be negative. The v mod q operation should yield a value between
1 and q - 1 inclusive.
See Change
notice No. 1
This appendix is for informational purposes only and is not required to meet
the standard.
Let L = 512 (size of p). The values in this example are expressed in hexadecimal
notation. The p and q given here were generated by the prime generation standard
described in appendix 2 using the 160-bit SEED:
With this SEED, the algorithm found p and q when the counter was at 38.
x was generated by the algorithm described in appendix 3, section 3.1, using
the SHA to construct G (as in appendix 3, section 3.3) and a 160-bit XSEED:
k was generated by the algorithm described in appendix 3, section 3.2, using
the SHA to construct G (as in appendix 3, section 3.3) and a 160-bit KSEED:
Finally:
Source:
http://csrc.nist.gov/fips/chnge186.htm
(Revised for use with FIPS 180-1)
This appendix is for informational purposes only and is not required to meet
the standard.
Let L = 512 (size of p). The values in this example are expressed in hexadecimal
notation. The p and q given here were generated by the prime generation standard
described in appendix 2 using the 160-bit SEED:
With this SEED, the algorithm found p and q when the counter was at 105.
x was generated by the algorithm described in appendix 3, section 3.1, using
the SHA-1 to construct G (as in appendix 3, section 3.3) and a 160-bit XKEY:
XKEY =
t =
x = G(t,XKEY) mod q
k was generated by the algorithm described in appendix 3, section 3.2, using
the SHA-1 to construct G (as in appendix 3, section 3.3) and a 160-bit KKEY:
KKEY =
t =
k = G(t,KKEY) mod q
h = 2
p =
q =
g =
x =
k =
k-1 =
M = ASCII form of "abc" (See FIPS PUB 180-1, Appendix A)
(SHA-1)(M) =
y =
r =
s =
w =
u1 =
u2 =
gu1 mod p =
yu2 mod p =
v =
3fe365cf 71c86224 12db6e7d d02bbe13 d88c58d7 263e9023
6af17ac8 a9fe5f24 9cc81f42 7fc543f7
25248b58 a3dc4f71 781d21f2 df89b717 47bd54b3 23bbecc4
43ec1d3e 020dadab bf782257 8255c104
9bb12d6c 628784fb 742e66ed 315754df e38b5984 e94d3725
37f655cb 3ea4767c 878cbd2d 783ee662
96b60b9c 1285b848 1d08505e 201a5c68 523a15ee 2fb62a56
d141dc4d 71925ef0 6acde0a5 b89c5671
0724a795 021bcd8c 93a39ddf 51cae380 fb6d682a 676608f7
65227ff0 5e44ccf4 9767e4a6 0832d33f
U.S. Department of Commerce
National Institute of Standards and Technology
Change No.: 1
Date of Change: 1996 December 30
Change Items:
"This algorithm can be used to precompute k, k-1, and r for m messages at
a time.
Algorithm:"
"This algorithm can be used to precompute k, k-1, and r for m messages at
a time. Note that implementation of the DSA with precomputation may be covered
by U.S. and foreign patents.
Algorithm:"
d5014e4b 60ef2ba8 b6211b40 62ba3224 e0427dd3
bd029bbe 7f51960b cf9edb2b 61f06f0f eb5a38b6
67452301 EFCDAB89 98BADCFE 10325476 C3D2E1F0
687a66d9 0648f993 867e121f 4ddf9ddb 01205584
EFCDAB89 98BADCFE 10325476 C3D2E1F0 67452301
Finally:
8df2a494 492276aa 3d25759b b06869cb eac0d83a fb8d0cf7
cbb8324f 0d7882e5 d0762fc5 b7210eaf c2e9adac 32ab7aac
49693dfb f83724c2 ec0736ee 31c80291
c773218c 737ec8ee 993b4f2d ed30f48e dace915f
626d0278 39ea0a13 413163a5 5b4cb500 299d5522 956cefcb
3bff10f3 99ce2c2e 71cb9de5 fa24babf 58e5b795 21925c9c
c42e9f6f 464b088c c572af53 e6d78802
2070b322 3dba372f de1c0ffc 7b2e3b49 8b260614
358dad57 1462710f 50e254cf 1a376b2b deaadfbf
0d516729 8202e49b 4116ac10 4fc3f415 ae52f917
a9993e36 4706816a ba3e2571 7850c26c 9cd0d89d
19131871 d75b1612 a819f29d 78d1b0d7 346f7aa7 7bb62a85
9bfd6c56 75da9d21 2d3a36ef 1672ef66 0b8c7c25 5cc0ec74
858fba33 f44c0669 9630a76b 030ee333
8bac1ab6 6410435c b7181f95 b16ab97c 92b341c0
41e2345f 1f56df24 58f426d1 55b4ba2d b6dcd8c8
9df4ece5 826be95f ed406d41 b43edc0b 1c18841b
bf655bd0 46f0b35e c791b004 804afcbb 8ef7d69d
821a9263 12e97ade abcc8d08 2b527897 8a2df4b0
51b1bf86 7888e5f3 af6fb476 9dd016bc fe667a65 aafc2753
9063bd3d 2b138b4c e02cc0c0 2ec62bb6 7306c63e 4db95bbf
6f96662a 1987a21b e4ec1071 010b6069
8b510071 2957e950 50d6b8fd 376a668e 4b0d633c 1e46e665
5c611a72 e2b28483 be52c74d 4b30de61 a668966e dc307a67
c19441f4 22bf3c34 08aeba1f 0a4dbec7
8bac1ab6 6410435c b7181f95 b16ab97c 92b341c0